[24회 실기]
PART1. 기계학습(50) - 메인 데이터 하나로 진행
1. Y(학생들의 결석 횟수) ~ X(부모님 동거여부, 부모님 학벌 클래스, 나이, ...)
1-1. EDA, 전처리
1-1-1. EDA 진행 시각화도 함께
head(data)
str(data) #data type
sum(is.na(data)) #NA여부 확인
barplot(data$y)#종속변수의 분포 확인
cor(data);plot(cor(data))#x간 상관관계(다중공선성), x,y의 상관관계1-1-2. 전처리 진행 시각화도 함께. 해당 전처리 과정이 분석 예측 결과에 어떤 영향을 미치는지도 설명
#NA 처리 1) 단순 대치법(completes analysis, 평균 대치법, 단순확률 대치법) 2) 다중 대치법
data$col <- iflese(is.na(data$col), mean(data$col, na.rm=T), data$col);
data[is.na(data$col), "col"] <- mean(data$col, na.rm=T)
#outlier 처리
boxplot(data$col) #이상치 처리 전 box plot 확인
LowerQ<-fivenum(data$col)[2];UpperQ<-fivenum(data$col)[4]
IQR<-IQR(data$col, na.rm=T)
upperlimit <- which(data$col<=UpperQ+1.5*IOQ);lowerlimit <- which(data$col>=LowerQ-1.5*IOQ)
data<-data[upperLimit&lowerLimit, "col"]
boxplot(data$col) #이상치 처리 후 box plot 확인
#normalization
normalize <- function(x, na.rm = TRUE) {
return((x- min(x)) /(max(x)-min(x)))
}
as.data.frame(apply(df$name, normalize))1-1-3. 시간이 부족해 못했지만 더 가능한 전처리 과정이 뭐가 있을까?
x변수들이 많아서 PCA를 통해 차원을 줄여 overfitting 완화, 그리고 변수들 조합으로 유의한 새로운 변수를 제안한다.
1-2. 알고리즘 적용
1-2-1. 해당 기계학습을 위한 방법론 3개를 제안하고 그 중 2개를 선택. 선택의 근거를 논리적으로 설명.
연속형 x와 연속형 y에 대한 알고리즘: 회귀모형
1) Linear(or Non linear depends on y~x corr) Regression
2) Lasso/Ridge Regression
3) Ensemble Regression(Random Forest, Bagging, Boosting)
1-2-2. 그 2개를 시행할 때 성능을 비교할 기준을 제안. 그 기준 선택에 대한 근거를 논리적으로 설명.
Adjusted R^2 score 로 비교 (cf. classification: ROC Curve, AUC, Accuracy etc.)
https://stherhj.tistory.com/182
1-2-3. 위에서 택한 2알고리즘에 대해 위에서 세운 성능 기준에 따라 비교하고 이를 시각화하여 표현할 것.
x에 대한 actual y과 predicted plot(predicted y)를 각각 찍어보이고 actual data set을 더 잘 estimate한 모형
1-3. 분석이 끝나고 이를 예측분석에 활용하기 전 단계에서
1-3-1. 해당 모델이 다른 환경에서도 활용가능하다는 것을 보여라. 시각화도 할 것
Hold Out 기법으로 train, test set을 나누어 train set으로 모델을 학습하고 test set에 대한 예측 adj R^2을 계산하고 plot을 그려 보여줌.
1-3-2. 이 외에 더 완전한 머신러닝모형이 되기위해 부수적인 방법들을 제안할 것.
variables selection : lasso ridge stepwise... 상황별 적절성 or x^2, ^3등 비선형 관계성 파악
PART2. 통계분석(50) - csv 파일로 저장되어있는 데이터는 제공X 각 작은 문제마다 샘플 제안
2. Y~x1, x2
2-1. 회귀계수 검정 (5)
glm돌려서 계수별 유의성
2-2. 모형 검정 (10)
F 통계량 확인, x변수 중 그 어느것도 Y에 유의한 영향을 미치지 못한다는 귀무가설을 기각
3. 두 모집단에 유의한 차이가 존재하는지 검정. 두 모집단이 정규분포를 따름,각 표본의 평균과 모집단의 분산 제시.
3-1. 귀무가설과 연구가설을 제시 (5)
H0: 두 모집단의 평균에 유의한 차이가 없다.
H1: 두 모집단의 평균에 유의한 차이가 존재한다.
3-2. 검정 진행하여 연구가설을 받아들일지 여부 제안 (10)
모집단의 정보를 알고 있으므로 독립표본 z-test를 진행한다. (모집단이 정규분포를 따르는건 t-test도 동일함.) 그러나 두 모집단의 분산이 서로 달라 등분산성이 보장되지 않음. A-B/(σ_A^2/n_A + σ_B^2/n_B)^1/2
4. 베이지안 확률 : 코로나 발병률이 0.01일 때 키트가 양성 떴는데 바이러스에 실제로 감염되었을 확률을 베이지안으로 구할 것. (15)

0.01*(370/(370+15))/(0.01*(370/(370+15))+0.99*(10/(10+690)))
https://stherhj.tistory.com/184
5. 모집단의 평균 길이를 알아내기 위해 표본 9개 뽑음 (z t = )
5-1. 해당 표본 값을 사용하여 모집단의 평균에 대한 신뢰구간 95% 구간을 제시. (5)
모집단 분산에 대한 정보가 없고 표본의 크기가 작으므로 t분포를 활용(모집단의 정규성을 가정).
5-2. 모집단의 분산이 0.04인 것을 나중에 알아냄. 이에 따른 신뢰구간 95% 구간을 제시. (10)
모집단의 정보를 알아 정규분포(z) 를 활용(모집단의 정규성을 가정)
[25회 실기]
PART1. 기계학습(50)
1. 온라인 유통회사 A사가 RMF(Recency, Monetary, Frequency) 중 F(고객의 구매 횟수) M (UnitPrice*Quantity) 기준 고객군집분석 시행 (25) (데이터 : CustomerID, InvoiceID, ProductID, Quantity, UnitPrice 등 제안)
1-1. EDA 이상치를 제거하고 필요하다면 변환도 적용 (5)
결측치 없는 데이터 확인, 먼저 unique InvoiceID에 cnt 1 열을 만들고 unique Customer ID 별로 sum하여 'F' 열 추가, 각 열 별 UnitPrice*Quantity 값을 Customer ID 별로 더하여 'M'열 추가. groupby.sum(Python)
data%>%group_by(CustomerID)%>%summarise(M=sum(UnitPrice*Quantity))이상치 제거(데이터 특성에 따라 UpperLimit 넘어가는 이상치만 제거), Frequency 대비 Monetary 열의 값의 range가 넓어 min max normalization 시행
1-2. 적합한 군집분석 알고리즘을 택하고 시행,결과에 대해 응집도와 분리도 관점에서 평가할 것 (10)
https://stherhj.tistory.com/202
k-means 군집분석 시행, 먼저 scree plot으로 최적의 군집 개수를 정하는데 2에서 elbow pt가 생겼지만 분석의 실효성을 위해 3으로 선정. within cluster sum of squares by cluster (between_SS / total_SS)로 전체 변동 중 군집 간 변동이 차지하는 비율 제시, 정분류율 추가 제시.
1-3. 각 군집의 특성을 제시하고 인사이트 제안.(5)
3개의 군집의 M, F 가 하나가 큰데 하나가 작고 한 경우 없이 모두 소-중-대 순으로 cluster mean 값이 확인되어 구매촉진프로모션 등 시행시 구매 횟수 혹은 장바구니 금액 둘 중 하나에 가중치를 두기 보다 같은 방향으로 구매 촉진 전략. 군집의 개수를 늘렸을 때도 같은 성향의 군집들로 구분되는 것을 확인함. (추가로 각 군집의 M, F의 수를 확인하여 프로모션 집중 구매 횟수, 금액대를 제안할 수 있었을듯)
2. 시기별 방문 고객수 데이터에 대한 시계열 분석 시행 (25)
2-1. EDA 시행, 시각화 (5)
시계열 그래프를 그리고 평균이 시간의 흐름에 따라 증가하는 추세를 보여 차분, 차분하고 나니 분산도 시간에 흐름에 따라 증가하여 변환하여 정상성 시계열 데이터 확보..차분+변환 전의 pacf와 이후의 pacf를 그려 완화됨을 보임.
2-2. 결측치 처리와 해당 결측치 처리 방식에 대한 논리적 근거 제시. (5)
딱 결측치가 3개!. 그래서 각 결측치의 직전, 직후 값의 평균 값으로 impute. 데이터의 평균값이 시간의 흐름에 따라 늘어나는 추세를 갖고 있어 전체 평균 값으로 대체하는 것이 비합리적이기 때문에 그 시점 즈음의 값으로 대체하는 것이 낫다고 판단함.(결측치가 여러 개 였으면 그냥 pad 방식으로 결측치 직전 값으로 채워넣을 수 있음, 직후는 bfill)
2-3. 계절성을 반영한 시계열 모델 적합하고 정확도 측면에서 모델 성능 평가할 것. (10)
SARIMA
2-4. 분석 결과 활용 가능 여부에 대한 분석 전문가로서의 제안. (5)
PART2. 통계분석(50)
3. 기본 통계 문제(20)
3-1. 서울에서 영동까지 100km/h로 가고 영동에서 서울까지 80km/로 돌아왔을 때, 평균 속도는? (5)
[조화평균] 속도 = 거리/시간 서울->영동 100km라고 했을 때 왕복 총 거리는 200km, 시간은 갈 때 1시간 올 때 1.25시간 (시간 = 거리/속도 = 100/80) 총 2.25시간 결국 평균 속도는 200km/2.25h = 약88.89km/h
3-2. 이전에 1000이었는데 올해 2000으로 늘고 내년에 3000으로 늘어날 예정이라면 평균 몇 배 증가한 것? (5)
[기하평균] 1000->2000->3000 2배 증가, 1.5배 증가 평균 r배 증가라면 매년 r배 증가 했을 때 했을 때와 같음. 2*1.5 = r*r, r=3^(1/2)
3-3. 남자 중 등산을 좋아할 확률은? (5)

P(남자&등산좋아)/P(남자)
3-4.20개 샘플링 했는데 분산이 90^2일때, 신뢰구간 95%에서 분산의 신뢰구간은? (5)
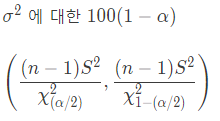
a/2= 0.025, n-1 = 19 s^2 = 90
lower_chi = qchisq(p=0.025, df=19, lower.tail=TRUE) #8.91
upper_chi = qchisq(p=0.975, df=19, lower.tail=TRUE) #32.85
19*90^2/lower_chi
19*90^2/upper_chi
4. 임상 대상 20명에 대해 혈압약 투약 이전과 이후의 차이가 24, 표준편차 9 신뢰구간 95%(10)
4-1. 귀무가설과 연구가설을 제시하시오. (5)
H0: 혈압약의 투약여부가 혈압에 대해 유의한 영향을 미치지 못한다.
H1: 혈압약의 투약여부가 혈압에 대해 유의한 영향을 미친다. (혈압약 투약 이전과 이후에 혈압에 유의한 차이가 있다.)
4-2. 검정 후 귀무가설 기각 여부 제시 (5)
모집단의 분산을 알지 못하고 샘플 사이즈가 30미만이므로 t-test 시행. 사전-사후 검사로 두 집단간 종속관계가 있으므로 종속표본(대응표본) t-test 시행. 먼저, 기각역 설정 t(0.025, 19)
qt(0.025, 19, lower.tail = TRUE) #-2.09
qt(0.025, 19, lower.tail = FALSE) #2.09
#[24-2.09*(9/20^(1/2)), 24+2.09*(9/20^(1/2))] = [19.79, 28.21]
24/(9/20^(1/2)) #검정통계량 t = 11.62 가 신뢰구간을 벗어나므로 H0를 기각하며 투약이 증상에 대한 유의한 영향을 미친다고 할 수 있다.
5. 공장 X,Y,Z의 중위값, 순위 (10)
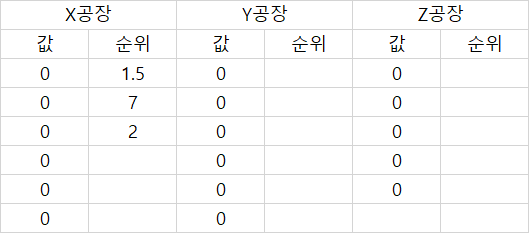
5-1. 귀무가설과 연구가설을 제시하시오 (5)
H0: X, Y, Z 공장의 집단의 평균이 모두 동일하다.
H1: X, Y, Z 공장 중 하나 이상의 공장의 평균값이 다르다.
5-2. 검정 후 귀무가설 기각 여부 제시 (5)
분산분석 ANOVA, but 모집단의 정규성 혹은 공장간 등분산성이 보장되지 않으므로 비모수 검정, 크루스칼 검정 진행
#R로 크루스칼-왈리스 검정해보기(kruskal.test() 함수) 예시
> A <- c(257, 205, 206, 231, 190, 214, 228, 203)
> B <- c(201, 164, 197, 185)
> C <- c(248, 165, 187, 220, 212, 215, 281)
> D <- c(202, 276, 207, 204, 230, 227)
> kruskal.test(list(A,B,C,D)) #결과는
Kruskal-Wallis rank sum test
data: list(A, B, C, D)
Kruskal-Wallis chi-squared = 6.839, df = 3, p-value = 0.07721#Python
stats.kruskal(X,Y,Z) #X, Y, Z는 rank가 아닌 raw data inputhttps://stherhj.tistory.com/158
6. A사에 투자하는데 1~5안의 투자 금액과 NPV(Net Present Value, 순현재가치) 를 제시. 최적의 투자안 선택. 1년차에는 50억, 2년차에는 60억, 3년차에는 80억을 투자한다고 했을 때 기대할 수 있는 NVP는?(10)
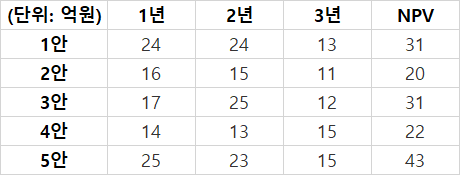
library(lpSolve)
#Max. Z = 31x1 + 20x2 + 31x3 + 22x4 + 43x5
z <- c(31, 20, 31, 22, 43)
# s.t.
# 24x1 + 16x2 + 17x3 + 14x4 + 25x5 <= 50
# 24x1 + 15x2 + 25x3 + 13x4 + 23x5 <= 60
# 13x1 + 11x2 + 12x3 + 15x4 + 15x5 <= 80
A <- matrix(c(24, 16, 17, 14, 25, 24, 15, 25, 13, 23, 13, 11, 12, 15, 15),nrow=3,byrow=TRUE)
B <- c(50, 60, 80)
dir <- c("<=", "<=", "<=")
opt <- lp(direction = "max", objective.in = z, const.mat = A, const.dir= dir, const.rhs = B, all.int=T)
opt #86
opt$solution #0 0 0 0 2https://stherhj.tistory.com/209
'쫌쫌따리 통계+데이터+AI' 카테고리의 다른 글
| [ADP] 이항분포/포아송분포 (0) | 2023.11.06 |
|---|---|
| 26회 통계 모음 (0) | 2023.03.10 |
| Google Cloud Certified - Professional Machine Learning Engineer (1) | 2022.09.09 |
| z검정, t검정 정리와 기출문제 (0) | 2022.08.29 |
| 시계열 분석(2) : 일보전진 이보후퇴 (0) | 2022.08.26 |



댓글