항상 나오기만하면 눈감고 저리가!!했던 시계열 분석..이젠 어쩔 수 없다ㅠㅠ친하게 지내보자..
시계열 데이터 구성 요소(original=trend+seasonal+random)
1. 추세변동(trend), 2. 순환변동(cycle), 3. 계절변동(seasonal), 4. 우연변동(random) : 백색잡음(white noise): 평균이 0이고 분산이 일정한 시계열 데이터의 노이즈
비정상성(non-stationary) 시계열 데이터 : 시간에 따라 평균과 분산이 변함(대부분의 시계열 자료 비정상성 시계열)
-(시계열 분석을 위해)->정상성(stationary) 시계열 데이터: 시간의 추이와 관계 없이 평균과 분산이 일정
1) 평균을 일정하게 : 차분(difference)-일반차분, 계절차분(데이터가 계절성을 갖는 경우)
(차분: 현 시점 데이터에서 d시점 이전 데이터를 뺸 것)
2) 분산을 일정하게 : 변환(transformation)
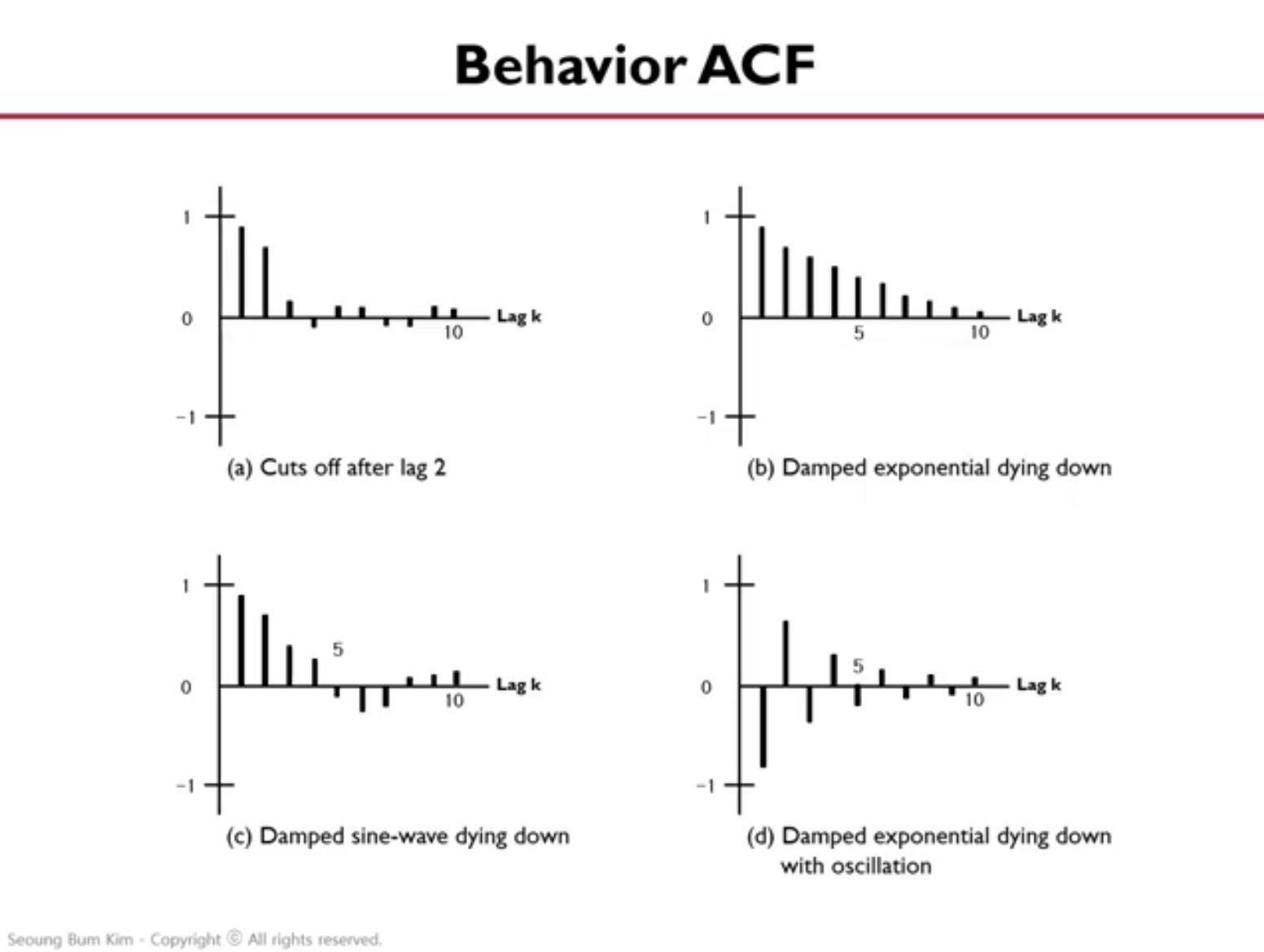
정상성 확인 : ACF plot을 활용 예: lag=1 자기자신과 한 시점 shift 데이터의 correlation (lag=0일 때는 1)
ACF가 패턴을 보이면 비정상성 데이터. 정상성: 빠르게 0에 수렴 비정상성: 천천히 변함
PACF: 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성(두 시점 사이의 다른 y의 영향력이 제거)
(나는 지금까지 ACF, PACF가 그 보더라인? 지나면 비정상성인줄 알았는뎁!ㅜㅜ)
ACF로 MA order개수(q) 결정, PACF로 AR order개수(p) 결정
*Ljung-box test 귀무가설: 자기 상관 계수들이 동시에 0과 같은 값을 가진다.
x <- rnorm (100)
Box.test (x, lag = 1)
Box.test (x, lag = 1, type = "Ljung")
자기회귀누적이동평균모형(ARIMA) : 비정상성 시계열 데이터를 differencing to secure stationarity 정상성을 위해 먼저 차분!! "integrated" 되었다.
-> 정상성을 가진 시계열 모형: 자기회귀모형(AR), 이동평균모형(MA), 자기회귀이동평균모형(ARMA) 을 활용하여 분석
AR(AutoRegressive) 모델 : Yt~x(yt-1...) Y의 과거 값들을 활용하여 스스로 t 시점의 Y를 예측. 일반 모형과 달라 계수를 추정할 때 최소제곱법 활용 불가능
MA(MovingAverge) 모델 : Yt~x(엡실론t...) 연속적인 에러텀을 활용해 t 시점의 Y를 예측.
->AR+MA = ARMA(AutoRegressive and MovingAverage) 모델 : Yt~x(yt-1...+엡실론t...)
ARIMA(p,d,q) : AR->p(t-p개: AR모델의 indep. order 개수) I->d(몇 번 차분?) MA->q (에러들..order 개수)
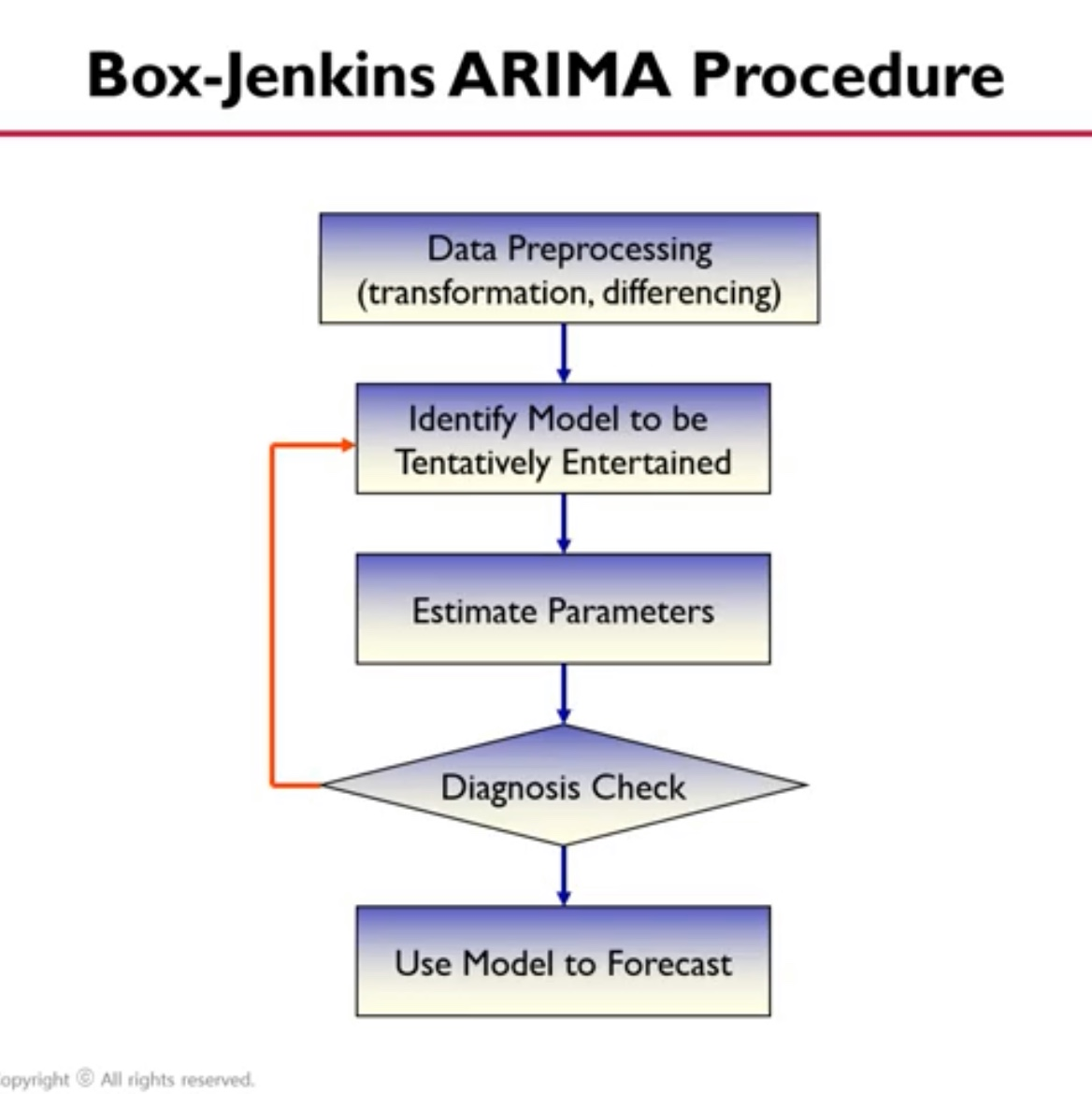
1. original data stationary 여부 확인! ACF 그려서 trend 확인.
2. 시범적 모델 찾아보기 acf pacf 를 확인하고 MA(q) AR(p) ARMA(p,q) 모델 중 선택(graphically)
otherwise, 컴퓨팅파워를 활용해 AIC나 testing data acc 확인하여 최적의 조합을 찾기

예: MA 모델, q=1로 선택 ARIMA(0,1,1) (0: AR 안해서 p 없 1: 차분 한 번해서 정상화 1: q=1)
ARIMA(0,1,2) 등 근방의 모델들 시도하여 AIC를 비교 (minimized 되어야함!) tentatively entertained
3. 파라미터 추정은??
4. diagnosis : residual의 3 sigma limit 한 두개 나와있는건 괜춘
5. forecating : 모형 고정 후 미래 값을 예측~
#시계열 자료 생성
tsdata <- ts(data, start = c(yr, month), frequency = 12)
acf(na.omit(tsdata), main="자기상관함수", col="red")
pacf(na.omit(tsdata), main="부분자기상관함수", col="red")
#비정상성 시계열 정상화
x11()
par(mfrow=c(1,2))
ts.plot(tsdata)
log <- diff(log(tsdata),differences = #)#로그 변환(for 분산 정상화) & 차분(for 평균 정상화) 수행
plot(log)
#시계열 자료의 추세선(평균, 분산 확인 가능) 시각화
ts.plot(tsdata, type='l",col="red)
#다중 시계열의 경우
plot.ts(cbind(tsdata$x1, tsdata$x2)), main="title")
#시계열 요소 분해 시각화
plot(stl(tsdata, "periodic")) #각 기본 data, seasonal, trend, remainder을 보임
m <- decompose(tsdata) #시계열분해
plot(m)
plot(tsdata-m$seasonal-m$trend) #계절, 추세 요인 제거 후에는 불규칙 요인만 존재
자기상관함수 ACF(Auto Correlation Function)
부분자기상관함수 PACF(Partial Auto Correlation Function)
차분된 시계열에 남아있는 자기상관을 수정하기 위한 AR항 또는 MA항이 필요한지 판단하기 위함
자기 과거 데이터에 현재 데이터가 영향 받으면 일정한 패턴을 보임(not random 자기상관성 존재).
ACF의 절대값이 임계치를 넘을 때 자기상관있음을 판단(lag=0 은 자기자신과의 관계로 1)
부분자기상관은 다른 변수 집합과의 상호 상관관계로 설명되지 않는 두 변수간의 순수한 상관관계파악
->있으면 어칸다구?
추세 패턴 찾기: trend를 찾고 선형 여부도 판단
SARIMA seasonal arima model 이전 ARIMA(p,d,q)(P,D,Q)s
월별 s=12 분기별 s=4
비계절적 요인과 비계절적 요인 총 7개
-
수정중(추가, 코드블럭으로 구분)
'쫌쫌따리 통계+데이터+AI' 카테고리의 다른 글
| 24회 ADP 데이터 분석 전문가 실기 (22/03/26) (0) | 2022.03.26 |
|---|---|
| 텍스트 마이닝(Term Document Matrix) (0) | 2022.03.24 |
| 유의성 검정(Significance Test) (0) | 2022.03.20 |
| 비모수적 검정 방법 (0) | 2022.03.20 |
| 데이터 처리 속도 측정 (코드 수행 시간 측정) (0) | 2022.03.20 |



댓글